La seguente pagina è rivolta a quanti mi hanno scritto per avere chiarimenti sull'argomento ed offre un altro esempio dell'uso della geometria frattale nei campi più inaspettati.
Esempi
Vediamo intanto che cosa si intende per interpolazione: abbiamo un certo numero di punti nel piano cartesiano e vogliamo costruire una funzione il cui grafico passi per ciascuno di questi punti. Per interpolazione frattale si intende la costruzione di un grafico che risulti un frattale, ovvero che sia autosimile.
La costruzione proposta è quella di Barnsley .
Procediamo per esempi e consideriamo tre punti di coordinante A (0 ; 1), B (2,5 ; 2) e C (5 ; 4). Nella figura 1 è disegnata in grigio anche la spezzata che si ottiene congiungendo i tre punti. La spezzata costituisce la figura A 0 di partenza.
| A 0 | A 1 | A 2 |
|
fig. 1 |
fig. 2 |
fig. 3 |
Cerchiamo di capire come sia possibile costruire una funzione passante per i tre punti il cui grafico sia un frattale. Consideriamo due trasformazioni geometriche che applicate alla spezzata, permettono di trasformarla nella figura A 1 formata da quattro segmenti.
Ciascuna delle due trasformazioni deforma in modo opportuno la spezzata di partenza. La prima trasformazione riproduce una copia della spezzata fra i punti A e B . La seconda trasformazione ne riproduce una copia fra i punti B e C . Applicando di nuovo le trasformazioni alla figura A 1 arriviamo alla figura successiva A 2 , costituita da una spezzata di otto segmenti.
Il risultato finale sarà la figura seguente, in cui abbiamo cancellato i passaggi intermedi:
Ovviamente possiamo scegliere infinite trasformazioni geometriche da applicare alla spezzata di partenza e questo permette di ottenere risultati finali molto diversi fra di loro. Vediamo due esempi, sempre considerando come figura di partenza la spezzata iniziale A 0 della figura 1.
|
|
|
|
|
|
|
|
|
|
|
|
Definizioni.
Le due trasformazioni affini che generano i frattali degli esempi precedenti hanno la seguente forma:
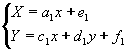 ;
;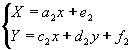 .
.Nota che nelle due trasformazioni i coefficienti b 1 e b 2 sono uguali a zero. Si tratta di una scelta operativa.
Per ricavare i coefficienti restanti, occorre risolvere un sistema di primo grado: si impone il passaggio della spezzata di ciascun passo per i vertici della spezzata del passo precedente.
In questo modo si determinano tutti i coefficienti tranne d 1 e d 2 . Questi ultimi restano indeterminati e possono essere scelti direttamente dall'utente. Di conseguenza esistono infinite curve frattali che interpolano i dati iniziali.
I coefficienti della curva passante per i punti dati A (x1 , y1) , B (x2 , y2), C (x3 , y3) sono i seguenti:
|
|
|
|
|
|
|
|
|
|
|
|
Per quanto riguarda i parametri d 1 e d 2 , essi sono i responsabili, nel senso che chiarirò dopo, della forma della curva. In ogni caso ha senso scegliere per i parametri d 1 e d 2 un valore compreso fra -1 ed 1.
Vediamo degli esempi per vedere come cambia la curva al variare dei parametri d 1 e d 2 . I primi tre casi sono quelli presentati sopra.
| N | d1 | d2 | Frattale |
| 1) | 0,5 | 0,5 |
|
| 2) | 0,6 | 0,8 | |
| 3) | 0,7 | -0,8 |
|
| 4) | 0,3 | 0,2 | 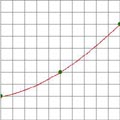
|
| 5) | -0,8 | -0,9 | 
|
| 6) | -0,95 | 0,9 | 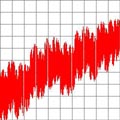
|
Dalla tabella risulta evidente il legame fra i parametri e il frattale finale.
Più il valore in modulo di tali parametri si avvicina ad 1, più il frattale risulta frastagliato e tende ad occupare più spazio.
Tali parametri determinano la dimensione del frattale.