Comandi di base Polinomi Grafica nel piano Grafica nello spazio Funzioni Equazioni differenziali

Grafica nello spazio

Comandi

Commenti

Rappresentazioni di curve nello spazio.
  • t= 0:pi/50:10*pi;
  • plot3(sin(t),cos(t),t)

Rappresentazione in tre dimensioni dell’elica di equazioni: x=sin(t); y=cos(t); z=t.
  • t= 0:pi/50:20*pi;
  • plot3(t.*sin(t),t.*cos(t),t)

Un altro esempio di elica. Si tratta di un’elica conica.
  • plot3(sqrt(t).*sin(t),sqrt(t).*cos(t),t)
  • plot3(t.^2.*sin(t),t.^2.*cos(t),t)

Altri esempi di eliche.
  • t = 0 : 2*pi/500 : 2*pi;
  • plot3((4+cos(10*t)).*cos(t), (4+cos(10*t)).*sin(t), sin(10*t))

Un esempio di elica torica.

Rappresentazione di superfici.
  • x=-1:0.1:1,
  • y= -1:0.1;1;
  • [X,Y]=meshgrid(x,y);

Vediamo come rappresentare una funzione del tipo z=f(x,y) nello spazio.

Il primo passo consiste nel creare una griglia di punti che costituiranno il dominio della funzione attraverso il comando meshgrid.

E’ raccomandabile usare il ; alla fine dei comandi.
  • Z=X.^2+Y.^2;
  • surf(Z)
  • surf(X,Y,Z)

Rappresentazione della funzione z= x2+y2. (paraboloide ellittico)
  • view(45,60)
  • view(45,90)

Rotazione dell’immagine. Il primo angolo esprime la rotazione orizzontale, il secondo l’elevazione verticale.
  • view(3)

Rappresentazione di default.

E’ equivalente a view(-37.5,30)

Per ruotare l’immagine è possibile agire anche direttamente sulla finestra del grafico.
  • mesh(Z)
  • mesh(X,Y,Z)

Rappresentazione della superficie tramite una rete.
  • contour(Z)

Mappa delle curve di livello della superficie. Questa rappresentazione è particolarmente utile nello studio dei punti critici di una funzione.
  • contour3(Z)

Mappa delle curve di livello in 3 dimensioni.
  • surfc(X,Y,Z)

Superficie e curve di livello.
  • surfl(X,Y,Z)

Superficie illuminata. La posizione della luce è quella di default.
  • surfl(X,Y,Z [60,30]))

Superficie illuminata con la posizione della luce specificata con i due angoli.
  • surf(X,Y,Z)
  • shading faceted
  • shading interp
  • shading flat

Le tre opzioni possibili per le sfumature dei colori. La prima è quella valida per default.
  • surfnorm(X,Y,Z)

Rappresenta la superficie ed i vettori normali ad essa.
  • axis off
  • axis on

Per nascondere o mostrare gli assi.
  • colormap cool
  • colormap hot
  • colormap gray
  • colormap pink
  • colormap(‘default’)

Scelta dei colori.
  • Z=X.^2-Y.^2;
  • surf(X,Y,Z)

Paraboloide iperbolico.
  • clear
  • x=[-1:0.1:1],
  • y= [-1:0.1;1];
  • [X,Y]=meshgrid(x,y);
  • Z=X.*Y+Y.*X.^2;
  • surf(X,Y,Z)
  • view(45,45)

Esempio di funzione polinomiale.
  • clear
  • x=[-pi:0.1:pi],
  • y= [-pi:0.1;pi];
  • [X,Y]=meshgrid(x,y);
  • Z=cos(X.^2+Y.^2);
  • surf(X,Y,Z)

Esempio di funzione trigonometrica. L’origine è un punto di massimo (relativo) per la funzione.
  • clear
  • x=[-1:0.1:1],
  • y= [-1:0.1;1];
  • [X,Y]=meshgrid(x,y);
  • Z=sin(X.*Y);
  • surf(X,Y,Z)

Altro esempio di funzione trigometrica.
  • clear
  • x=[-1:0.1:1],
  • y= [-1:0.1;1];
  • [X,Y]=meshgrid(x,y);
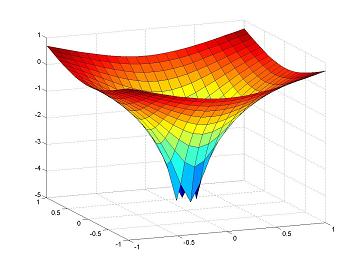
  • Z=log(X.^2+Y.^2);
  • surf(X,Y,Z)

La funzione non è definita nell’origine.
  • clear
  • x=[-1:0.1:1],
  • y= [-1:0.1;1];
  • [X,Y]=meshgrid(x,y);
  • Z=1-sqrt(X.^2+Y.^2);
  • surf(X,Y,Z)

Esempio di funzione irrazionale. Nota il punto angoloso.
  • clear
  • x=[-2:0.1:2];
  • y= [-2:0.1;2];
  • [X,Y]=meshgrid(x,y);
  • Z=exp(-X.^2-Y.^2);
  • surf(X,Y,Z)

Esempio di funzione esponenziale. Nota il punto di massimo.


  • hold on
  • zm=max(max(Z))
  • [pos_xm , pos_ym]=find( Z==zm );
  • xm=diag( X(pos_xm,pos_ym) )
  • ym=diag(Y(pos_xm,pos_ym))
  • h=plot3(xm,ym,zm,'.');
  • set(h,'color',[1 1 0],'markersize',25)

Ricerca del punto di massimo e sua messa in evidenza nel grafico della funzione precedente.

Ricerca delle posizioni nella matrice Z in cui si trova il valore massimo

Ricerca delle coordinate corrispondenti alle posizioni in cui e' stato trovato il valore massimo.

Evidenzio il punto di massimo nel grafico.

Sotto il risultato ottenuto:

esempio
  • Z=Y.*exp(-X.^2-Y.^2);
  • surf(X,Y,Z)
  • contour(X,Y,Z)

Confronta il grafico con il caso precedente. La funzione possiede punti di max/min?
  • Z=X.*Y.*exp(-X.^2-Y.^2);
  • surf(X,Y,Z)
  • contour(X,Y,Z)

Confronta il grafico con il caso precedente. La funzione possiede punti di max/min?
  • Z=(X.^2+3*Y.^2).*exp(1-X.^2-Y.^2);
  • surf(X,Y,Z)
  • contour(X,Y,Z)
  • surf(X,Y,Z)
  • view(45,45)
  • view(60,60)

Studiare i punti di max e min della funzione. Usa il comando view.

Si tratta di una funzione con due punti di massimo, un punto di minimo e due punti di sella.
  • Z=exp(-X).*(X.*exp(-X)+cos(Y));
  • surf(X,Y,Z)

L’intervallo scelto per gli assi non permette una corretta visualizzazione.
  • clear
  • x=[-0.5:0.1:2],
  • y= [-10:0.1;10];
  • [X,Y]=meshgrid(x,y);
  • Z=exp(-X).*(X.*exp(-X)+cos(Y));
  • surf(X,Y,Z)

Cambiando gli intervalli, si può vedere che si tratta di una funzione con infiniti massimi locali ma senza alcun punto di minimo. Non sono presenti nemmeno punti di sella.
  • [ X, Y] = meshgrid( -2 : .1 : 2 );
  • Z= X.^2 + Y.^2;
  • surf( X, Y, Z )
  • hold on
  • z = 2*X + 2*Y - 2;
  • surf( X, Y, Z )

Disegniamo nella stessa finestra due funzioni usando il comando hold on.

Si tratta di un paraboloide e di un piano tangente alla superficie.

Superfici in coordinate parametriche.
  • [ u, v ] = meshgrid( -2 : .1 : 2 );
  • x = u;
  • y = v.^2;
  • z = u .* v;
  • surf( x, y, z )

Vediamo come disegnare una superficie definita tramite delle equazioni parametriche del tipo:

x=f(u,v)

y=g(u,v)

z=h(u,v)

dove u e v sono parametri reali.

Consideriamo come esempio la superficie algebrica di equazione definibile anche attraverso le equazioni parametriche x=u, y=v2,z=uv.
  • a=-3:0.1:3;
  • b=0:0.1:3*pi;
  • [u,v]=meshgrid(a,b);
  • x=(25+u.*sin(v./2)).*cos(v);
  • y=(25+u.*sin(v./2)).*sin(v);
  • z=u.*cos(v./2);
  • surf(x,y,z)
  • shading flat

Il Nastro di Moebius.
  • a=0:0.1:3*pi;
  • b=0:0.1:3*pi;
  • [u,v]=meshgrid(a,b);
  • x=(15+2.5.*cos(v)).*cos(u);
  • y=(15+2.5.*cos(v)).*sin(u);
  • z=2.5.*sin(v);
  • surf(x,y,z)
  • shading flat

Un toro.

Sfere.
  • clear
  • sphere(10)
  • sphere(30)

Il comando sphere permette di generare una sfera.
  • [X,Y,Z]=sphere(15)
  • surf(X,Y,Z)
  • surfl(X,Y,Z)
  • surfl(X,Y,Z,[40,80])

In questo modo viene prima generata una matrice di punti appartenenti alla sfera.

Cilindri e solidi di rotazione.
  • [X,Y,Z]=cylinder(10)
  • surf(X,Y,Z)

Per disegnare un cilindro.
  • t=0:0.1:2*pi;
  • [X,Y,Z]=cylinder(2+cos(t))

Il comando cylinder permette anche di disegnare la superficie di rotazione generata da una curva in rotazione intorno all’asse delle z.

 

Esercizi

 e studiarne il comportamento nell’origine.

a cura di: Laura Lotti - e-mail:webmaster@frattali.it - Ultima revisione: 17 novembre 2003