Vediamo come si può risolvere il problema di Cauchy:
.
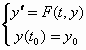function z=funzione(t,y)
z=t
Esempio 1:
Consideriamo il seguente caso banale:
.
La soluzione cercata è 
.
Per risolvere il problema con Matlab, occorre innanzitutto definire una funzione di due variabili in un M-file come a fianco. Il file deve essere salvato come funzione.m
- tstan=[0 10]
E’ necessario definire un intervallo di integrazione.
Nell’esempio cerchiamo una soluzione nell’intervallo [0,10].
- [t,y]=ode23(‘funzione’,tstan,1)
L’istruzione usata, ode23, è bastata sul metodo di Runge-Kutta del 2 e 3 ordine.
- [t,y]=ode45(‘funzione’,tstan,1)
L’istruzione usata, ode45, è bastata sul metodo di Runge-Kutta del 4 e 5 ordine.
- t
- y
Vengono mostrati a schermo i valori di t e di y (soluzione numerica dell’equazione). Il programma non fornisce l’espressione della soluzione del problema di Cauchy ma un insieme di valori numerici da essa assunti.
- plot(t,y)
Grafico della soluzione trovata
- polyfit(t,y,2)
Polinomio interpolatore di 2 grado.
function F=odefile(t,y)
F=F(t,y)
Sintassi generale per un M-file per la risoluzione del problema di Cauchy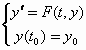 
.
Il file deve essere salvato come odefile.m
- tstan=[to tfinal]
- [t,y]=ode23('odefile',tstan,y0 )
- [t,y]=ode45('odefile',tstan,y0 )
La sintassi generale per la risoluzione del problema di Cauchy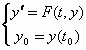 
è quella a fianco.
Nota che t0 è l’estremo sinistro dell’intervallo.
function z=funzione2(t,y)
z=y-t
Esempio 2.
Studiamo il seguente problema di Cauchy:
.
Si tratta di un’equazione differenziale del primo ordine.
L’integrale generale è y=cex+x+1. L’integrale particolare è y=x+1.
Definiamo un M-file come a fianco (salvandolo come funzione2.m).
- tstan=[0 5]
- [t,y]=ode23(‘funzione2’,tstan,1)
- [t,y]=ode45('funzione2',tstan,1)
- t
- y
- plot(t,y)
Ricerca della soluzione.
Nella maggior parte dei problemi il comando ode45 è da preferire al comando ode23 poiché garantisce una precisione superiore.
function z=funzione3(t,y)
z=[y(2);t.^3-2-y(1)]
Esempio 3.
Risolviamo ora un’equazione differenziale del secondo ordine.
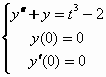
Per risolverla, occorre trasformarla in un sistema di due equazioni del primo ordine nel seguente modo:
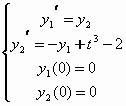
dove abbiamo posto y1=y e y2=y’
L’integrale generale è y(t)=Acos(t)+Bsin(t)+t3-6t-2.
La soluzione particolare del problema di Cauchy è y(t)=2cos(t)+t3-6t-2.
Definiamo un M-file come a fianco e salviamolo come funzione3.m
Nota che la funzione cosi’ definita è una funzione vettoriale nelle variabili t e y. y è una matrice formata da due colonne y(1) e y(2).
- tstan =[0 5]
Intervallo di integrazione
- y0=[0 0]
Condizioni iniziali di y e y’.
- [t,y]=ode23('funzione3',tstan,y0);
Soluzione.
- plot(t,y)
Grafico di y e di y’.
- plot(t,y(:,1))
Grafico della soluzione
Con y(:,1) ci riferiamo alla prima colonna della matrice y.
- plot(t,y(:,2)
Grafico della derivata.
Con y(:,2) ci riferiamo alla seconda colonna della matrice y.
function z=funzione4(t,y)
z=[y(2);y(2).*(1-y(1).^2)-y(1)]
Esempio 4.
Risolviamo ora un’altra equazione differenziale del secondo ordine.
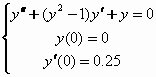
Per risolverla, occorre trasformarla in un sistema di due equazioni del primo ordine nel seguente modo:
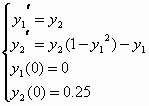
dove abbiamo posto y1=y e y2=y’
Definiamo un M-file come a fianco e salviamolo come funzione4.m
- tstan=[0 5]
- y0=[0 0.25]
- [t,y]=ode23(‘funzione4’,tstan,y0);
- plot(t,y)
Risoluzione dell’equazione.
function z=funzione5(t,y)
z=t.*(y-y.^3)
Esempio 5.
Risolvere il seguente problema di Cauchy:
.
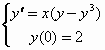(Si tratta di un’equazione differenziale di Bernoulli. A fianco l’M-file corrispondente.)
function z = vdp1000( t , y )
z = [y(2) ; 1000*(1-y(1).^2).*y(2)-y(1)];
tstan=[0 3000]
y0=[2 0]
[t,y] = ode15s(‘vdp1000’,tstan,y0);
plot(t,y(:,1));
Esempio 6.
Consideriamo l’equazione di Van der Pol:
y''- m (1-y2)y'+y=0
che governa l’intensità di corrente in un circuito oscillante a triodo. Consideriamo in particolare il caso critico che si ha per m =1000:
y''-1000(1-y2)y'+y=0
Procedendo come negli esempi precedenti, si scrive il seguente sistema equivalente all’equazione data:
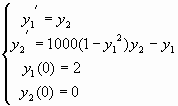
Il corrispondente M-file è quello a fianco che deve essere salvato come vdp1000.m
Per la risoluzione di questa equazione i metodi visti fino ad adesso si rivelano però inadeguati dal momento che la soluzione cercata è una funzione che varia con estrema rapidità. Il comando da usare in questo caso è ode15s dove s indica "stiff".