Definizioni
Una rotazione è un tipo particolare di trasformazione affine. Vediamo come è definita.
Nel caso di una rotazione in senso antiorario di un angolo
, le equazioni analitiche della rotazione sono le seguenti:
.La matrice della trasformazione vale:
Notiamo che
Proprietà fondamentali.
Si può dimostrare che una rotazione delle seguenti proprietà:
- l'unico punto unito è l'origine;
- una rotazione trasforma una figura geometrica in una figura congruente a quella data.
Esempio
Consideriamo la seguente rotazione
T
secondo un angolo di 30 gradi
ovvero di
:
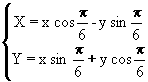
Per capire come agisce T , vediamo come viene trasformato da T il triangolo isoscele ABC (nelle figura rappresentato in rosso) di vertici A(0,1), B(-1,0), C(0,-1). Il punto A ha come immagine il punto A'(-0.5,0.9). Il punto B ha come immagine il punto B'(-0.9,-0.5). Il punto C ha come immagine il punto C'(0.5,-0.9).
|
|
Notiamo che la figura trasformata (nel disegno il triangolo in blu) è un triangolo congruente a quello di partenza.