Nota sulla definizione di trasformazione affine.

Cerchero' di spiegarti meglio.

Consideriamo due piani e e un'applicazione T , ovvero una legge, che fa corrispondere ad ognuno dei punti P(x, y) di uno ed un sol punto P'(X,Y) di .
Per dire brevemente questo, si dice che l'applicazione è una funzione fra i due piani.

Ma affinché la nostra applicazione sia un'affinità questo non basta. Prima di tutto T deve essere biiettiva . Questo vuol dire che ogni elemento di deve avere una ed una sola controimmagine in .

Poi dobbiamo richiedere qualcosa di più su come è fatta l'applicazione. Come devono essere legate le coordinate di P' a quelle di P ? Ovvero come si ottengono le coordinate X e Y dalle x e y ?
La risposta è la seguente: (*) dove a, b, c, d, e, f sono numeri reali.
Dire che ci garantisce che T sia biiettiva. Questo numero a volte viene chiamato determinante dell'applicazione.
Vediamo degli esempi:

Esempio 1

L' applicazione T definita da è un'affinità. Infatti ad - bc = -1. Se vuoi saperne di più vai alla pagina sulle trasformazioni affini .

Esempio 2

L'applicazione T definita da non è un'affinità. Infatti ad - bc = 0.

Esempio 3

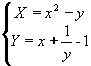L'applicazione T definita da non è un'affinità poiché non è della forma richiesta sopra nella formula (*) .